How to graph
Type your complex function into the f(z) input box, making sure to include the input variable z. Then hit the Graph button and watch my program graph your function in the complex plane! If it graphs too slow, increase the Precision value and graph it again (a precision of 1 will calculate every point, 2 will calculate every other, and so on). Click on a point on the graph to see the exact output of the function at that point—you can also double click on the value of the z label on the right-hand pane to enter an exact input point. (Confused? Read about complex numbers below!)
About Complex Numbers
Here's my basic explanation. Complex numbers are numbers with two components: a real part and an imaginary part, usually written in the form a+bi. The number i, while well known for being the square root of -1, also represents a 90° rotation from the real number line. As such, a complex number can represent a point, with the real part representing the position on the horizontal, real number line and the imaginary part representing the position on the imaginary or vertical axis.

Operations with complex numbers use the properties of i to transform these points. For example, if we square the complex number 2+3i, we expand (2+3i)(2+3i) and get 4 + 12i - 9 = -5 + 12i. When we multiplied the 3i by 3i, the is multiplied into -1. Points represented as complex numbers are numbers like any other, and just like with real numbers, we can define functions that take in a complex number and output another complex number. But graphing complex functions is a lot harder than graphing normal functions. Why? A normal function takes in a number x and outputs a number y. But a complex function takes in a complex number, or point, z and outputs another complex number w. We'd need four dimensions to graph a point to a point!
One solution to this is called complex domain coloring, and that's what I've implemented in this project. Domain coloring makes every input complex number a point on a 2D graph, and every output complex number a color. It then colors each input point with its cooresponding output color. How do we choose a color for a complex number? If you imagine the complex number as a triangle like below, it has an angle θ. A number like 1+1i will have a θ of 45°, because if you move 1 unit to the right and 1 unit up you made a 45° slope. Similarly, 0+0i will have a θ of 0°, 0+1i will have a θ of 90°, and 0-1i will have a θ of 270°.
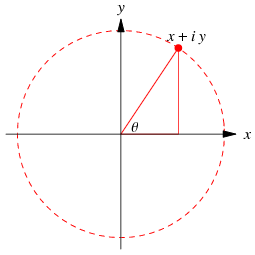
A complex number also has a magnitude, or absolute value: the distance away from the origin. This is the hypotenuse of the triangle above. You can find this by simply using the Pythogorean Theorem using the real part and the imaginary part as the two known sides. For example, |3+4i| = \sqrt{3^{2}+4^{2}} = 5, meaning 3+4i is 5 units away from the origin.
Once we know our angle and magnitude, we can use those values to make a color. In HSL (hue, saturation, and lightness) color, the hue is between 0 and 360, just like our angle θ, so we set the hue of the color to the θ. We want the color to be fully saturized, so we set the saturation to 100%. Finally, we set the lightness based on the magnitude, so that the further away the complex number is from the origin, the lighter it is. 0+0i is completely black. Undefined or "not a number" results are graphed gray.
If you graph the identity function f(z) = z in my program, you can see exactly what color gets mapped to each point. Positive real is red, negative real is cyan, positive imaginary is light green and negative imaginary is deep purple, with beautiful complex numbers everywhere in between.
Functions to try
f(z) = z
f(z) = (z + 2i)(z - 2i)
f(z) = \frac{1}{z}
f(z) = \log(z)
f(z) = \sin(z)\tan(z)
f(z) = e^{z}
f(z) = gamma(z)
f(z) = \sin(e^{z})
f(z) = \sin(\log(z))
These functions have large portions of their graphs that graph infinity:
f(z) = \log \left(\sin \left(e^z\right)\right)
f(z) = \cos \left(z\right)^{e^z}
f(z) = gamma(z)^{gamma(z)}
Credits
My project uses Mathquill for the amazing LaTex rendering, and Mathjs for complex number calculations. Also thanks to my friends Matthew Sklar, Shaun Regenbaum, and Ezra Blaut for testing, and of course to Mr. Shillito for introducing me to the beauty of complex numbers in the first place.